BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLERİ ÇÖZME
Evet arkadaşlar denklemler nasıl kurulur gördük.
İşte şimdi yapmamız gereken ise kurduğumuz denklemleri doğru bir şekilde çözebilmek. Tabiki denklemi doğru kurduğunuzdan emin olarak

Denklem Çözme Yöntemleri
Denklemler, bilinmeyenlerine göre ve derecelerine göre sınıflandırılmaktadır.
Cebirin temeli olarak kabul edilirler. Denklem kurma ve denklem çözme problemleri en sık olarak 7. sınıfta ve 9. sınıfta karşımıza çıkmaktadır. Fakat hemen hemen her sınavda denklemler ile karşılaşacaksınız. O yüzden iyi kavramak ve iyi uygulamak çok önemli. Bu yazımızda birçok denklemin çözüm yöntemini anlatacağım ama adım adım, tane tane gideceğiz...
İlk olarak yapmamız gereken, denklemlerde bilinmeyenleri ve bilinenleri aynı tarafta toplamak.Sonra bir taraftan diğer tarafa geçirirken işaretin değişeceğini bilmek. Sonrası dört işlem aslında.
Denklem Çözme Yöntemleri Nelerdir?
Denklem çözümünde aşağıdaki özeliklerden yararlanırız.
*Bir eşitliğin her iki tarafına aynı sayı ilave edilirse eşitlik bozulmaz.
a = b ise, a + c = b + c dir.
*Bir eşitliğin her iki tarafından aynı sayı çıkarılırsa eşitlik bozulmaz.
a = b ise, a – c = b – c dir.
*Bir eşitliğin her iki tarafı aynı sayı ile çarpılırsa eşitlik bozulmaz.
a = b ise, a × c = b × c dir.
*Bir eşitliğin her iki tarafı sıfırdan farklı aynı sayı ile bölünürse eşitlik bozulmaz.

*Bir eşitliğin her iki tarafının n. kuvveti alınırsa eşitlik bozulmaz.
a = b ise, an = bn dir.

*(a = b ve b = c) ise, a = c dir.
*(a = b ve c = d) ise, a ± c = b ± d dir.
*(a = b ve c = d) ise, a × c = b × d dir.
*

*a × b = 0 ise, (a = 0 veya b = 0) dır.
*a × b ¹ 0 ise, (a ¹ 0 ve b ¹ 0) dır.
*

Birinci dereceden bir bilinmeyenli denklem çözüm yolları.
x ɛ R olmak üzere, mx + n = 0
Şeklindeki ifadelere, 1. Dereceden bir bilinmeyenli denklem denir. m ve n sayılarına denklemin katsayıları, x sayısına ise denklemin bilinmeyeni denir. Denklemin çözümünü sağlayan her x reel sayılarının oluşturduğu kümeye de denklemin çözüm kümesi denir.
1. Dereceden bir bilinmeyenli denklemlerin en sade şekli yukarıdaki ifadedir.Denklem çözme yöntemlerinde ilk amacımız, denklem üzerinde çeşitli işlemler yaparak denklemi en sade haline getirerek mx +n = 0 şeklinde yazabilmektir.
Bir denklemi mx +n = 0 şekline getirdik. Sonra ki işlemimiz ise x bilinmeyenin çarpan olarak bulunduğu sayıları,eşitliğin bir tarafına, sabit katsayıları yani bilinen sayıları da eşitliğin diğer tarafına almak olmalıdır.Bunu yaparken işaretlere çok dikkat etmeliyiz.
mx + n =0 eşitliğinde,n eşitliğin sağ tarafına alınır ve -n olarak geçer. Eşitliğin sol tarafından sağ tarafına bir sayı alınırken işareti değiştirilir. Yine eşitliğin sağ tarafından sol tarafına bir sayı taşınırken, sayı işaret değiştirmektedir. (mx = -n)
Bir denklemin her iki tarafı da aynı sayıya bölünebilir. Unutmayalım ki,bu bölme işlemi denklemin değerini,oranını ve sonucunu değiştirmez.
mx / m = -n/m işlemini uygulayıp, x sayısını yalnız bırakmamız lazım. Eşitliğin sol tarafında pay ve paydada aynı m sayısı var..X'in önündeki m sayısı sadeleşir ve x= -n/m olur.Böylece denklemdeki bilinmeyen olan x sayısı bulunmuş olur. Şimdi birkaç örnek ile konuyu daha anlaşılır bir hale getirelim.
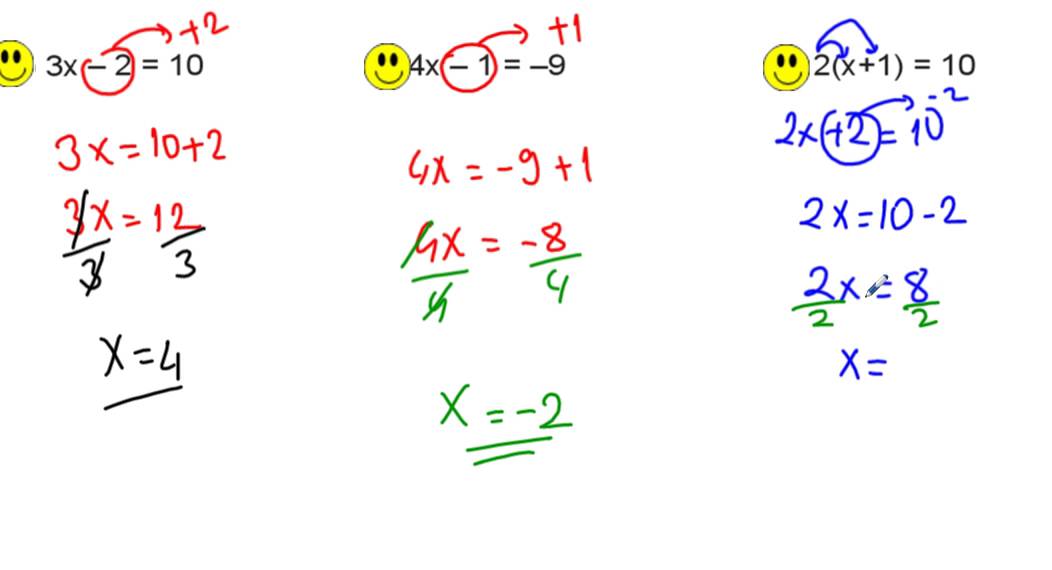
Örnek;
5x -4 = 16Denkleminde bilinmeyen x sayısı kaçtır?
Çözüm5x -4 = 16 ifadesinde (-4) sayısını eşitliğin sağ tarafına taşıyacağız. Böylece bilinmeyen x sayısını yalnız bırakmak için, çarpan olarak bulunduğu 5x ifadesinin eşitliğin solunda kalmasını sağlayacağız. Eşitliğin sağ tarafında oluşan sabit sayılar (+4) ve (16) toplanacak.
5x = 16 + 4
-4 sayısı eşitliğin sağ tarafına taşınırken işareti değişti ve (+4) oldu. Denklem, 5x = 20 halini aldı. x bilinmeyen sayısını bulmak için denklemin her iki tarafını da 5'e böleceğiz. Yani aslında X'in katsayısı ne ise (-) veya (+) olduğuna dikkat ederek böleceğiz.
5x/5=20/5 ve bu durumda x = 4 olacak ve böylece denklemin çözüm kümesini bulmuş olacağız.
Örnek
-3x + 13 + 5x -7 = -4 + 7x -9 Denkleminde bilinmeyen x sayısı kaçtır?
ÇözümHer zamanki gibi denklemde bilinmeyen x sayılarını bir tarafta, sabit katsayıları ise bir tarafta toplayacağız. Burada X'i sol tarafta veya sağ tarafta toplayabiliriz sonuç değişmez. Kafanız karışmasın yani sadece bir tarafta mı toplamam lazım diye düşünmeyin. Ben X sayılarını sağ da, bilinenleri ise solda toplayacağım bu sefer.
Sol da oluşacak sayılarımız 13 - 7 + 4 + 9 olurken, sağ tarafta oluşan sayılarımız 7x + 3x -5x olacaktır. Bu durumda 13 - 7 + 4 + 9 = 7x + 3x -5x olur. Şimdi iki tarafı da düzenleyelim ve 19=5x eşitliğini elde edelim. X'in katsayısı 5 olduğundan her iki tarafı da 5 sayısana bölelim. 19/5 = 5x/5 olur. Bu durumda X'in önündeki 5 ile payda da bulunan 5 sadeleşir ve x=19/5 olacaktır. Size güzel bir problem ve çözümünü bırakıyorum.


Birinci dereceden iki bilinmeyenli denklem çözüm yolları.
x,y ɛ R olmak üzere, mx + ny + k = 0 denklemine birinci dereceden iki bilinmeyenli denklem denir. Burada x ve y bilinmeyenler, m,n,k ise katsayılardır. Bu birinci dereceden iki bilinmeyenli denklemler düzlemde bir doğru belirtir unutmayalım.Bu oluşan doğru üzerindeki bütün x ve y noktalarının oluşturduğu ikililer ise denklemin çözüm kümesidir. Sonuç olarak mx + ny + k = 0 denkleminin çözüm kümesi birçok ikiliden oluşabilir.Birden fazla iki bilinmeyenli denklemden oluşan sistemlere ise birinci dereceden iki bilinmeyenli denklem sistemi denilmektedir.
 Denklem sistemlerinin ise birçok denklem çözme yöntemi vardır.
Denklem sistemlerinin ise birçok denklem çözme yöntemi vardır.
Birinci dereceden iki bilinmeyenli denklemlerin çözüm kümesinin bulunmasıBirinci dereceden iki bilinmeyenli denklem sistemlerinin çözüm kümesi bulurken birçok yol kullanılır. Yok etme yöntemi,karşılaştırma yöntemi, yerine koyma yöntemi,grafik yöntemi,determinant yöntemi gibi yöntemlerden biri yardımı ile denklem çözülür. Bu yöntemlerden en fazla üçü kullanılır ve bende size bu üçünü anlatacağım.
a. Yok Etme Yöntemi: Değişkenlerden birini yok ederek, diğer bilinmeyeni bulmak için kullanılır. Diğer bilinmeyeni bulduğumuzda ise denklemlerden birinde yerine koyarak diğer bilinmeyen bulunur.
Bir örnek ile açıklayalım.
3x - 2y = 6
-2x + 4y = -4 denkleminin çözüm kümesini bulunuz.
İlk olarak hangi bilinmeyeni yok edeceğinize odaklanın ve genelde daha kolay yok edeceğiniz veya soruda sizden istenen bilinmeyenin kalacağı şekilde yok etmeyi uygulayabilirsiniz. Bu iki denklemi alt alta toplayacağımız için -2y'nin olduğu bütün denklemi 2 ile çarpıp alttaki 4y ile toplandığında y bilinmeyenlerinin yok olmasını sağlayabiliriz.
Denklemi çarpacağımız sayı bütün denklemi etkiler unutmayalım. Şimdi 2 ( 3x - 2y = 6 ) yapacağız ve denklem 6x - 4y = 12 denklemine dönüşecek. Bu durumda;
6x - 4y = 12
-2x + 4y = -4
bu denklemler oluşur. Eşitliğin sol tarafını toplayarak bir tarafa, sağ tarafını toplayarak bir tarafa yazacağız. Bu durumda 6x-4y-2x+4y=12-4 olacaktır. Düzenleme yaparsak, 4x=8 olur ve x=2 olacaktır. Şimdi üstteki veya alttaki denklemde yerine koyabiliriz. Ben ilk baştaki üstteki denklemde yerine koyuyorum. 3 (2) -2y = 6 olur. Düzenleyelim 6-2y=6 olacaktır. ve -2y=0 olur. Bu durumda her tarafı 2'ye bölersek y=0 olacaktır.
 b. Yerine Koyma Yöntemi:
b. Yerine Koyma Yöntemi: Verilen denklemlerin birinden, bilinmeyenlerden biri çekilip diğer denklemde yerine yazılarak sonuca gidilir.
Aynı örnek ile açıklayalım.
3x - 2y = 6
-2x + 4y = -4 denkleminin çözüm kümesini bulunuz.Burada x sayısını veya y sayısını üstteki ya da alttaki denklemde yalnız bırakıp diğer denklemde yerine koymamız gerekmektedir. Ben üstteki x sayısını yalnız bırakıp alttaki x gördüğüm yere yazacağım.
3x=6+2y ve her iki tarafı 3'e bölersek x=(6+2y)/3 olacaktır. Şimdi altta yerine yazarsak,
-2(6+2y)/3 + 4y = -4 bu denklem oluşur. Düzenleme yapalım, (-12-4y)/3 +4y=-4 olur.Şimdi y sayısını yalnız bırakmaya çalışalım. 4y ve -4 sayısını 3 ile çarparsak her taraf sade hale gelecektir. Yani -12-4y+12y=-12 olur. Düzenlersek 8y=0 yani y=0 olacaktır.
 c. Karşılaştırma Yöntemi:
c. Karşılaştırma Yöntemi: Verilen denklemlerin ikisinden de aynı değişkene odaklanarak çekilir.Sonra denklemlerin diğer tarafları karşılaştırılır yani aslında eşitlenir.Her iki denklemden de aynı değişken kolayca çekilebiliyorsa, "Karşılaştırma yöntemi"kolaylık sağlar.
Aynı örnek ile açıklayalım.
3x - 2y = 6
-2x + 4y = -4 denkleminin çözüm kümesini bulunuz.
Burada x sayılarını yalnız bırakalım ve taraf tarafa ayıralım.
3x=6+2y
-2x=-4-4yBirinci tarafta x'lerin katsayılarını eşit tutmalıyız. Yani ilk denklemi 2 ile, ikinci denklemi -3 ile çarparak düzenleyelim.
6x=12+4y
6x=12+12y olacaktır. Bu durumda 12+4y=12+12y olur. y=0 olduğu bu şekilde de görülmüş olur.

İkinci dereceden bir bilinmeyenli denklem çözüm yolları.
İlk olarak sizlere 2. dereceden bir bilinmeyenli denklem ne demek bunu anlatmaya çalışacağım. Aslında yine yapmamız gereken bilinmeyeni artık soruda hangi harf ise o bilinmeyen onu bulabilmek. Sadece bu durumda bilinmeyenin derecesinin iki olduğunu unutmamak gerekiyor. Yani o bilinmeyenin eğer çözümü varsa iki tane kökü olduğunu bileceğiz.
Bakınız bu denklem gibi x²+3x+2=0 
Bu denklemler genel olarak ax²+bx+c=0 olarak gösterilmektedir. Bilinmeyen x ve a,b,c katsayılardır. 

