Matematikte geçmişten bu güne kadar değiştirilemeyen birtakım kurallar vardır. Bunlardan bir tanesi de bir sayıyı asla sıfıra bölemeyeceğinizdir. Sayı sıfıra bölündüğünde sonsuz mu yoksa tanımsız mı sorusunu yanıtlayacağımız yazımızda sizlerle birlikteyiz.Matematik başlı başına ilginç bir bilim dalı, çünkü doğanın en kadim gizemlerine ışık tutuyor. Kimine göre zor kimine göre ise oldukça eğlenceli bir ders olan matematikte
sıfır sayısının da özel bir yeri var. Zira akıldan çıkmayan matematik kurallardan biri de bir sayıyı sıfıra bölemeyeceğinizdir.
Reel sayılarda, yani sayı doğrusundaki bütün sayılar kümesinde bir sayının
sıfır ile bölümü bize okullarda tanımsız diye öğretildi. Peki neden bir sayıyı sıfıra bölerseniz sonuç tanımsız olur hiç merak ettiniz mi? Gelin isterseniz bu sorunun cevabına birlikte bakalım.
Bir sayı neden 0'a bölünmez?
Herhangi bir reel sayının sıfıra bölümü tanımsızdır. Bölme işleminde sıfır ile bölüm tanımlı değildir. Ayrıca sonsuz da değildir. Bölümün sonucu pozitif sonsuz ya da negatif sonsuz olabilir. İki sonsuz da bir reel sayı belirtmez, dolayısıyla kesin olarak söyleyebiliriz ki,
sayı bölü sıfır tanımsızdır.
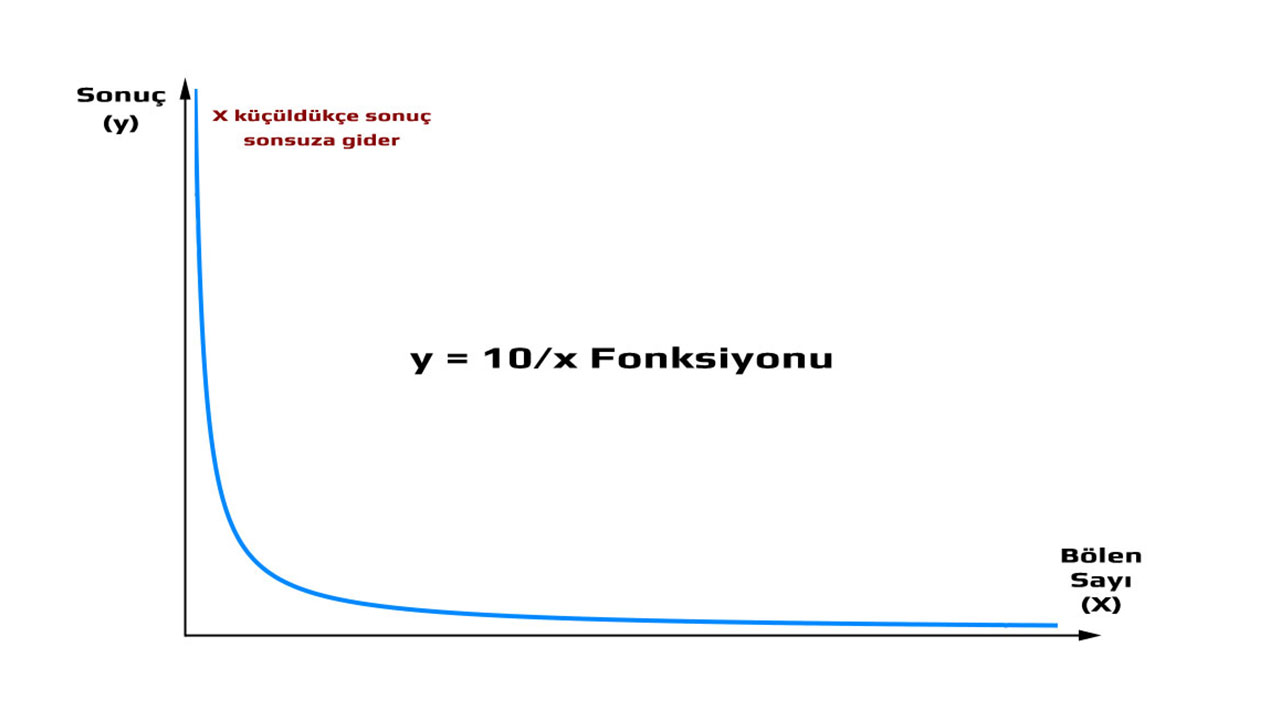
Mesela 10 sayısını sıfıra böldüğünüzde elinize ne geçtiğini düşünmek için; 10'u 5'e bölmekle başlayalım. Bu işlemin
cevabı 2 olur. Peki ya 10'u daha ufak bir rakamla, 2'yle bölseydiniz ne olurdu? Daha
büyük bir sayı olan 5'i elde ederdiniz. Peki ya 10'un 1'e bölünmesi?

Yine daha büyük bir rakam çıkar. 10. ½'ye bölünen 10, 20 eder. ¼'e bölündüğü zaman 40; 1/32'e bölündüğü zamansa 320 yapar. Ne zaman
daha ufak bir sayıya bölseniz, karşılığında daha büyük bir sayı elde edersiniz. Yani, bölen sayı 0'a ne kadar yaklaşırsa; cevabınız o kadar sonsuzluğa yaklaşır. Bu yüzden aslında 10'u 0'a bölseydiniz, sonsuzluk elde ederdiniz değil mi?
Bu işlemde bir sonuç almak adına
yalnızca limit alabilirsiniz. (Sayı / X), x giderken sıfıra şeklinde ve bu fonksiyonun davranışını inceleyebilirsiniz. Ancak burada da karşımıza tek bir limit değeri çıkmaz, çünkü limitler sağdan ve soldan farklıdır.Sıfıra sağdan yaklaşırken, fonksiyonun değeri pozitif olarak sonsuza doğru gider. Sonsuz bir kısaltmadır, anlamı ise, sonucun herhangi bir X reel sayısından yüksek olduğu, sürekli büyüdüğü ve dolayısıyla hiçbir zaman belli olmadığıdır. Tek söyleyebileceğiniz, istediğiniz her reel sayıdan büyük bir sonuç elde edebileceğinizdir.
 Sıfıra soldan yaklaşırken
Sıfıra soldan yaklaşırken ise, durum negatif yönde aynıdır. Sayı mutlak değerce çok büyür ancak negatifdir, dolayısıyla
küçülür.Belirleyebileceğiniz herhangi bir negatif reel sayıdan daha küçük bir sayıdır, dolayısıyla eksi
sonsuzdur denir. Söylediğimiz gibi, X/0'ın hiçbir değeri yoktur, tanımlı bir
işlem değildir. Sıfır ile asla bölme yapamazsınız.
Zaten sonsuz da reel sayılar kümesinde
tanımlı bir sayı olmadığından, kesin olarak tanımsızdır. Sıfır bölü sıfır, bir üzeri sonsuz, sonsuz bölü sonsuz, sonsuz eksi sonsuz birer belirsizliktir. Tanımsız değildir. Bu işlemleri yapabilmek için belirsizliğe neden olan durumu ortadan kaldırıp sonucu bulabiliriz.
Sıfıra bölme işlemi,
yanıtını bulamadığınız bir işlemdir, bu nedenle işlemin sonucu tanımsızdır. Bölme ve çarpmanın birbiriyle arasındaki ilişkiye bakacak olursak nedenini anlayabilirsiniz. 6'yı 3'e bölerseniz, cevap 2'dir, çünkü 2 çarpı 3 = 6 olur. 6'yı sıfıra bölerseniz, "Sıfır çarpı 6'yı hangi sayı verir?" Sorusunu sorarsınız. Bunun cevabı elbette bir sayı değildir, çünkü herhangi bir gerçek sayının sıfır çarpı sıfırın 6 olmadığını biliyoruz. Bu yüzden
sıfıra bölmenin tanımsız olduğunu söylüyoruz, çünkü diğer sayılarla bölme tutarlı değildir.
Riemann Küresi ve Stereografik Yansıtma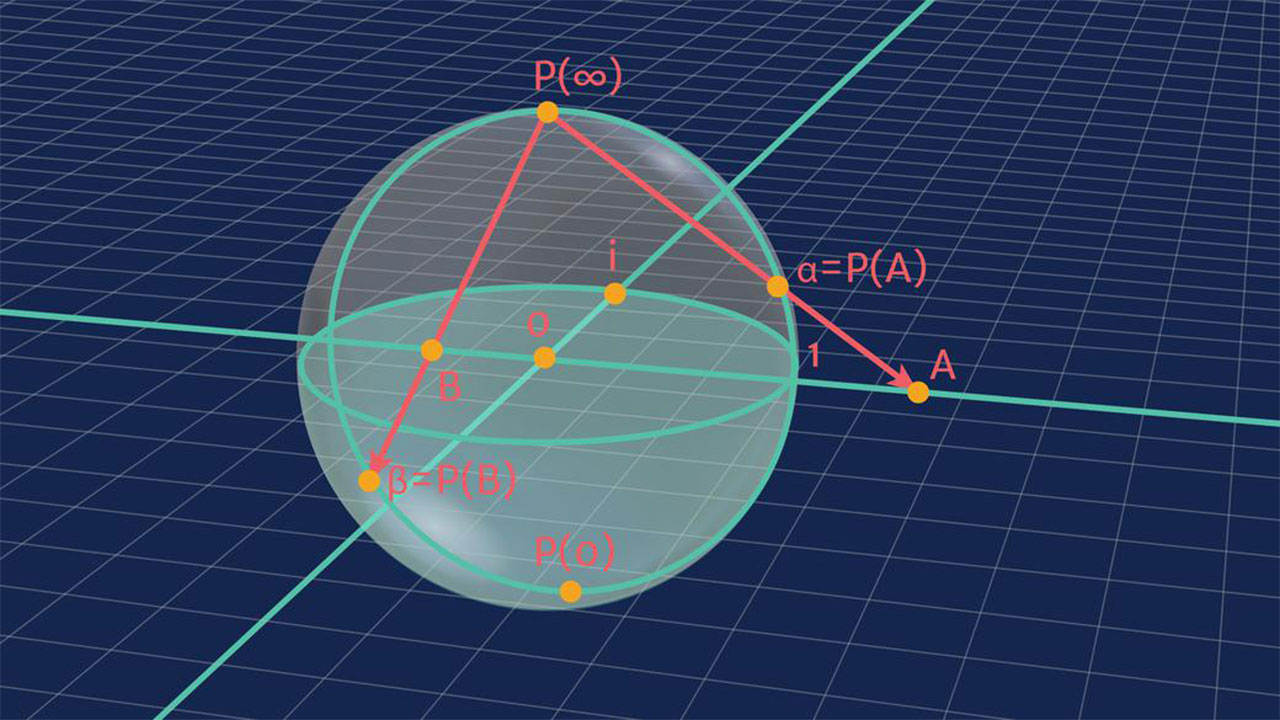
Düşünün ki,
tüm yönlerde sonsuzluğa giden ve ortada bir merkezi bulunmayan iki boyutlu bir düzlem var. Şimdi bu düzlemi büküp küreye çevirdiğinizi ve sıfırın güney kutbu olduğunu, köşelerin de en tepede; kuzey kutbu olan yerde birleştiğini hayal edin. Şimdi, bir başka sonsuz iki boyutlu düzlem alın ve onu ekvatoru kesecek şekilde yerleştirin. Bu düzlem üzerinde seçtiğiniz
herhangi bir nokta, kürenin Kuzey Kutbu'na düz bir çizgiyle bağlanabilir. Eğer seçtiğiniz nokta, kürenin dışındaysa; bağlantı çizgisi küreyle kuzey yarımkürede kesisecek. Eğer kürenin içerisindeyse, güney yarımkürede kesisecek.
Hayal ettiğiniz şey, bir
Riemann Küresi. Düzlemdeki her noktayı, küredeki bir kesişim noktasıyla ilişkilendirmeyi kapsayan bu yönteme
stereografik yansıtma deniyor. Temel olarak, düzlem üzerinde bulabileceğiniz herhangi bir noktayı küre üzerinde bulabilirsiniz.
Buna sonsuzluk da dahil. Düzlemde sonsuzluğa ne kadar yaklaşırsanız, kürenin Kuzey Kutbu'na da o kadar yaklaşırsınız.
Başka bir örnekle açıklayacak olursak; Portakallara elma eklerseniz ne olur?
Portakallara elma eklerseniz ne olur? Elbette bir anlam ifade etmiyor, bu yüzden en kolay şey, mantıklı olmadığını veya bir matematikçinin dediği gibi,
"tanımsız" olduğunu söylemektir. Belki de ona bakmanın en iyi yolu budur. Matematikte,
"XYZ işlemi tanımsız" gibi bir ifade gördüğünüzde, bunu kafanızda
"XYZ işlemi bir anlam ifade etmiyor"şeklinde düşünebilirsiniz.
Bunu düşünmenin başka bir yolu da bir kutuyu elmalarla doldurmayı hayal etmektir. Bir kutuda 100 elma olduğunu varsayalım. Şimdi bu elmaların yarısı büyüklüğündeki elmalarla doldurmayı deneyin. Kutuya 200 tane elma koyabilirsiniz. Şimdi hiç yer kaplamayan özel,
sihirli bir elma hayal edin. Kutuya kaç tane koyabilirsiniz?
Bu işlemin
herhangi bir cevabı yok. Bu nedenle matematikçiler 0'a bölünen sayıları
"tanımsız" olarak adlandırır. Bazı araştırmacılar bu işlemi sonsuz olarak görme eğilimindedir, ancak bu işlem tam olarak doğru değildir. Öncelikle bir sayının sıfıra bölümü ilk bakışta sonsuz gibi düşünülebilir. Çünkü bölen sayı küçüldükçe sonuç büyür. Örneğin 10 sayısını her adımda daha küçük sayılara bölersek sonucun büyüdüğünü görürüz.
- 10 / Bölen Sayı = Sonuç
- 10 / 1 = 10
- 10 / 0,1 = 100
- 10 / 0,01 = 1000
- 10 / 0,001 = 10000
- 10 / 0,0001 = 100000
- 10 / 0,00001 = 1000000
- 10 / 0,000001 = 10000000
- Bağıntı = 10/x = y
Gördüğünüz gibi bölen sayı ne kadar
küçük olursa sonuç o kadar büyük olmaktadır. Yani bölen sayı sıfıra yaklaştıkça sonuç da sonsuza yaklaşmaktadır. O halde bir sayının sıfıra bölümü sonsuz olmalıdır.

Bu durumun neden doğru olmadığını anlamak için öncelikle bölme işleminin ne ifade ettiğini bilmemiz gerekir. Örneğin 10 sayısını 2 sayısına böldüğümüzde sonuç 5 çıkar. Bu işlem bize 10'un içinde kaç tane 2 olduğunu gösterir. Ayrıca bölme işlemi matematiksel olarak çarpma işleminin tersidir. Bölme ve çarpma işlemlerinin sonucunu birbirine eşit olacak şekilde düzenlersek çarpımsal ters kavramı ortaya çıkar.
- 10 / 5 = 2 = 10 x 1/5
- 10 / 2 = 5 = 10 x 1/2
- 10/a = 10 x 1/a
İşlemlerdeki 1/a sayısına çarpımsal ters denir. ilk işlemde 5'in çarpımsal tersi 1/5, ikinci işlemde 2'nin çarpımsal tersi 1/2'dir. Yani bir sayının çarpımsal tersi 1'in bu sayıya bölümüdür
(a'nın çarpımsal tersi 1/a 'dır). Peki çarpımsal ters ne işimize yarayacak? Bir sayının çarpımsal tersi ile çarpımı daima 1 sonucunu verir.
- Sayı x Çarpımsal Ters = 1
- 5 x 1/5 =1
- 2 x 1/2 = 1
- 4000 x 1/4000 = 1
- a x 1/a = 1
Bu durumda sıfırın çarpımsal tersi 1/0 olmalı ve çarpımsal tersi ile çarpımı da 1'i vermelidir
(0 x 1/0 = 1). İşte sorun burada ortaya çıkar. Çünkü bir sayının sıfır ile çarpımı sıfırdır. Bu nedenle sıfırın çarpımsal tersi yoktur. Yani 1/0 tanımsızdır. Sayıların sıfıra bölüm işlemlerini çarpım olarak yazarsak
- 5/0 = 5 x 1/0
- 10/0 = 10 x 1/0
- -3/0 = -3 x 1/0
1/0 tanımsız olduğu için bütün sonuçlar tanımsızdır. Yani bir sayının sıfıra bölümü tanımsızdır. İlk kısımda bahsettiğim ve mantıklı gibi görünen
1/0 = Sonsuz düşüncesi hala mantıklı gibi gelebilir. Fakat bu durum negatif sayılar için de aynı sonucu vermektedir. Bir sayıyı sıfıra yaklaşan negatif sayılara böldüğümüzde sonuç eksi sonsuza yaklaşır.

- 10 / Negatif Bölen Sayı = Sonuç
- 10 / -1 = -10
- 10 / -0,1 = -100
- 10 / -0,01 = -1000
- 10 / -0,001 = -10000
- 10 / -0,0001 = -100000
- 10 /- 0,00001 = -1000000
- 10 /- 0,000001 = -10000000
- Bağıntı = 10/-x = -y
Bu nedenle 1/0 sonucu sonsuz ise 1/-0 sonucu da eksi sonsuz olmalıdır. Sıfır nötr bir sayı olduğundan 1/0 için hem artı sonsuz hem de eksi sonsuz sonuçları ortaya çıkar. Artı sonsuz ile eksi sonsuz birbirine eşit olmadığından
bu düşüncenin yanlış olduğu görülür.
Bütün bu işlemler kafanızı karıştırdıysa
basit bir mantık üzerinden gidelim. Önceki kısımlarda bahsettiğim gibi örneğin 10/5 işlemi 10'un içinde kaç tane 5 olduğunu gösterir. Buna göre 10/0 işlemi 10'nun içinde kaç tane sıfır olduğunu göstermelidir. 10'un içinde kaç tane sıfır vardır? 1, 10, sonsuz... bilmiyoruz çünkü sonuç matematiksel olarak tanımlanmamıştır. Bu nedenle bir sayıyı sıfıra bölersek sonuç tanımsızdır.
Bu yazımızda sizlerle bir sayının neden sıfıra bölünemediğini tüm detaylarıyla açıklamaya çalıştık. Meraklıları için faydalı olduğunu düşündüğümüz bu yazıda, bir sayıyı sıfıra böldüğümüzde neler olur, sonuç
tanımsız mı yoksa sonsuz mu sorularına yanıt aradık. Bir sonraki yazımızda buluşuncaya dek sağlıcakla kalın.


